Una questione di completezza – Scacchi, sistemi linguistici e sistemi formali

Iscriviti alla Newsletter!

---

Uno scorpione voleva attraversare un fiume e chiese ad una rana di portarlo. “No”, disse la rana “no grazie. Se ti portassi sul dorso tu potresti pungermi e la puntura di uno scorpione è mortale”. “Ma, non è logico” disse lo scorpione, gli scorpioni cercano sempre di essere logici “se io ti pungessi, tu moriresti e io affogherei.” La rana si convinse e lasciò che lo scorpione gli salisse sul dorso. Ma proprio nel bel mezzo del fiume la rana sentì un dolore terribile. Si rese subito conto che lo scorpione l’aveva punta. “E la logica?” chiese la rana nel mentre che incominciava a discendere verso il letto del fiume insieme allo scorpione “Non è logico quello che hai fatto”.“Lo so” disse lo scorpione “ma non posso farci nulla. E’ il mio carattere.”[1]

Orson Welles

---

Vuoi leggere un libro sulla filosofia degli scacchi? Un mistero in bianco e nero – La filosofia degli scacchi!

Ho sentito e letto critiche ai danni di quei pochi, ma importanti, “sistemi scacchistici”, critiche che si sviluppano attorno a due nuclei argomentativi distinti. Uno è lo scetticismo sulla qualifica delle mosse (definite in termini di “buone” o “cattive”), l’altro è l’osservazione che qualunque sistema di scacchi si sia dimostrato incompleto o, ancora peggio, incoerente.

Incompletezza e incoerenza sono due proprietà generali dei sistemi logici (i così detti “sistemi formali”): posto che un linguaggio prevede la formazione di frasi ben costruite, allora un sistema è completo se dimostra una frase o la sua negazione. Ad esempio, nel linguaggio degli scacchi, una frase come “la regina è in d1” o è vera o è falsa e, perché il linguaggio degli scacchi sia completo, deve poter dimostrare che o “la regina è in d1” è vera oppure deve dimostrare che è vera la sua negazione. Il linguaggio della scrittura delle mosse (che è un linguaggio a tutti gli effetti) è sicuramente completo perché consente sempre di dimostrare se “1) Dd1” è vera oppure è falsa: basta guardare la lista delle mosse di una partita e vedere dove sta la donna. Se la donna è alla mossa 1 in D1 allora è vera, altrimenti è falsa. Facile.

D’altra parte, non c’è solo il criterio di completezza ma anche il criterio di coerenza: un linguaggio è coerente solo se non dimostra contraddizioni. Anche in questo caso, possiamo dire che il linguaggio della scrittura delle mosse è senz’altro coerente perché non dimostra mai contraddizioni. In questo senso, possiamo dire che abbiamo un linguaggio di scrittura delle mosse che è coerente e completo.[2]

Ma è evidente che questo linguaggio è poverissimo! Non ci dice assolutamente niente di interessante. Ad esempio, non ci dice quali varianti avremmo dovuto giocare, quali mosse erano perdenti, quali vincenti. Faccio un esempio tratto, una volta tanto, dalla mia pratica di gioco:

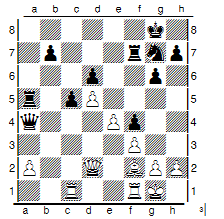
In questa posizione il Bianco gioca “27) e5”. La mossa è buona o cattiva? C’erano alternative e, se c’erano (e c’erano) erano rilevanti? Con il nostro linguaggio scacchistico non lo possiamo dire: banalmente, nel formulario non compare la possibilità di dirlo. Così ci costruiamo un linguaggio più potente, che incorpora anche la possibilità di indicare varianti alternative che inseriamo tra parentesi quadre, proprio per indicare (con una convenzione intuitiva) che la partita sarebbe potuta andare diversamente. Le parentesi quadre sarebbero traducibili in parole come “è possibile che…”, cioè operatori logici modali (possibilità/necessità etc.) che ci dicono “esiste una partita possibile che, identica fino a qui a quella giocata, sarebbe potuta andare in questo modo”. Le partite possibili negli scacchi sono molte, ma non infinite, però sono talmente tante che non possiamo elencarle tutte: quante parentesi quadre (possibilità) sarebbero state “apribili” nella posizione che ho fornito? Al bianco sono possibili 36 mosse, cioè 36 possibilità alternative, inclusa quella giocata. Nell’insieme ho considerato anche quelle palesemente irrilevanti, come “27) DxTa5”. Ma la rilevanza non dipende né direttamente né indirettamente dalla possibilità di una mossa. Se non vogliamo limitarci a parlare dei fatti, cioè di tutto ciò che accade e di tutto ciò che non accade, dobbiamo necessariamente ampliare il regno di ciò che vogliamo dire, vale a dire la “bontà”, la “rilevanza” di mosse e varianti. La rilevanza è indicata implicitamente dalla selezione di una certa variante: se c’è, se è possibile, allora, per i criteri del commentatore, è rilevante. Sebbene questa non sia una “teoria della rilevanza”, ci dà qualche informazione intuitiva sulla sua “realtà”. Mentre è di ben altra consistenza il problema della “bontà”.

Si badi bene che potremmo benissimo fare a meno di includere il concetto di “bontà” e “cattiveria” nel nostro linguaggio; e il nostro linguaggio sarebbe coerente e completo. Solamente che di questa sua coerenza e completezza non sapremmo che farcene, se non che, ad esempio, vogliamo dimostrare all’arbitro che abbiamo ragione noi nel dire che il nostro avversario ha giocato una mossa illegale (lo possiamo dimostrare con certezza proprio perché il nostro sistema deduttivo non impone errori).[4] Ma quante volte capita? A me è successo una sola volta in dieci tornei! E quante volte capita di voler parlare di alternative e volerle qualificare? Tutte le volte.

Allora ampliamo il nostro linguaggio e introduciamo due nuovi simboli: “!” e “?”. Non ci interessano gli altri perché sono tutti riducibili a questi due. Naturalmente, per ottenere gli altri ci servono delle regole che ci dicano come usarli. Sono talmente semplici che molto spesso non pensiamo neppure che esistano, ma ci sono e ci serve anche una “interpretazione” che ci dica “cosa significano” i simboli. I simboli, infatti, di per sé non significano nulla!: la regola è “interpreta il segno ! come buono” e “interpreta il segno ? come cattivo“. Le regole di combinazione sono, invece: “prendi il simbolo !, prendi il simbolo ?; se metti il simbolo ? a destra di ! hai un nuovo simbolo!?” Questa è una regola di formazione di un nuovo simbolo. Non c’è niente di difficile, niente di strano. A questo punto abbiamo un nuovo linguaggio che è costituito da quello vecchio, con i nuovi simboli “!” e “?” (il tema della costruzione di un linguaggio verrà approfondito nel primo capitolo del mio nuovo libro che uscirà tra qualche mese). Questo linguaggio è ancora completo e coerente? E qui sta il grande problema. Se riusciamo a stabilire che il linguaggio nuovo è incoerente, allora abbiamo dimostrato che è incompleto. A me non interessa stabilire formalmente se lo sia, ma è evidente che ci servirebbero delle regole esplicite di deduzione che ci consentano di dimostrare che “27) e5!” è vera oppure falsa. Esiste un simile sistema di deduzione?

I sistemi scacchistici classici come Il mio sistema adottano il linguaggio di scrittura delle mosse o suoi equivalenti (sono equivalenti tutti i linguaggi che dicono la stessa cosa, così il linguaggio della scrittura delle mosse è equivalente alla notazione descrittiva, quella che ti dice: metti un pedone di fronte al re, il re è nella casa di partenza etc.,).[5] Ma ne Il mio sistema Nimzowitsch non solo assume questo linguaggio di base, ma assume anche quello superiore con i simboli “!” e “?” e, in realtà, ne assume uno ancora più “ricco”, perché usa anche simboli (o parole che stanno per essi) di valutazione di varianti (“+”, “-” e combinazioni). Quello che Nimzowitsch fa, a differenza di molti altri, è fornire una serie slegata di “regole di deduzione” che ci dicono quando ad una mossa si può associare il simbolo “!” e quello “?”. Il buon Nimzowitsch, come il buon Tarrasch, vivono durante quel periodo della Storia dell’umanità (i primi tre decenni del secolo scorso) nel quale si voleva dare un fondamento a tutta la scienza, compresa la matematica, attraverso sistemi di deduzione, simili ai famosi Elementi di Euclide. Essi usano, dunque, dei linguaggi che includono: mosse, proprietà delle mosse, varianti, valutazioni di varianti. D’altra parte, anche così, il linguaggio rimane molto povero e noioso, motivo per il quale tutti gli scacchisti usano la loro lingua naturale per parlare di scacchi.

Qual’è il punto? E’ dimostrabile logicamente che sistemi alla Nimzowitsch, che usano una logica dei predicati del secondo ordine (semplicemente: si possono dire cose come “-27) e5- ha tutte le proprietà per essere una buona mossa”) sono incompleti e incoerenti! Vale a dire che non solo dimostrano le frasi scacchistiche vere, ma anche false! Questo perché i linguaggi completi e coerenti sono una minima parte e sono, come si dice, molto poveri: parlano di pochissime cose, in modo esaustivo e coerente, ma non dicono niente di interessante. E allora abbiamo bisogno di linguaggi più forti ma, purtroppo, imperfetti. Non solo! Per i famosi teoremi di Gödel, si può anche dimostrare che i problemi dei sistemi come quelli di Nimzowitsch siano dovuti a un inconveniente: esiste almeno una frase del loro linguaggio che è indimostrabile, cioè non si può dire né che sia vera, né che sia falsa, pur essendo formulabile dal buon Nimzowitsch! In altre parole, Il mio sistema ammette almeno una frase che, sebbene sia costruibile, essa non è dimostrabile. Si tenga ben presente che tutto ciò è una parziale forzatura, che assume la possibilità di ridurre Il mio sistema a qualcosa di logicamente ben formulabile. Il che, comunque, era nelle idee dell’autore, almeno parzialmente.

Abbiamo fornito, apparentemente, una ragione fortissima per dubitare (a livello conoscitivo) della validità di tutti i sistemi che vogliano parlare delle proprietà degli scacchi perché o sono così poco espressivi che non dicono nulla (ma sono completi e coerenti) oppure dicono molto ma sono incompleti e incoerenti. Ma è veramente importante tutto ciò? Io direi di no, anzi, direi che non ha nessuna importanza.

Il motivo è che gli scacchisti, specie gli scettici e i critici dei sistemi a la Nimzowitsch, non hanno in mente una visione logica, deduttiva. Essi si pongono esclusivamente il problema di trarre un vantaggio pratico dalla lettura di simili testi. Il fatto che abbiano, magari, tratto motivo per dubitare li conduce a mettere in discussione in blocco i risultati dei “sistematori”. Ma questo non ha molto senso, proprio perché loro non hanno in mente lo sviluppo di un sistema che sia altrettanto capace di dimostrare verità scacchistiche, ma solo che sia utile. Uno dei miei più grandi rammarichi, da conoscitore della Storia degli scacchi, è che non ci sia mai stata una “ricerca scientifica collettiva” che abbia guidato i giocatori e che li abbia animati da uno sforzo comune alla ricerca di una teoria simile a quella di Nimzowitsch: troppo egoismo, troppa volontà di svettare, troppo poco interesse collettivo degli scacchisti, troppo agonismo. Ad esempio, sarebbe stato più utile dire “le premesse di N. sono tutte valide eccetto la numero 1 (faccio per dire), dunque, dobbiamo trovare un nuovo principio che vada bene” e continuare fino alla formulazione di una buona teoria. Ma lo scopo è vincere, battere l’avversario. Come non ha importanza. E allora i sistemi ritornano utili, fino a che non mostrano i loro limiti e, senza dubbio, i loro vantaggi sono superiori agli svantaggi, anche quando si sia dimostrato che essi sono logicamente incompleti e incoerenti. Attenzione! Il fatto che siano logicametne incompleti e incoerenti vuol dire che dicono anche cose scacchisticamente false, ed è questo il punto rimarcato dai critici. Dal canto mio, essi aiutano a capire gli scacchi, molto più che a dimostrarli, e, per questo, ben venga il buon Nimzowitsch, che, a distanza di quasi un secolo, rimane una delle più valide fonti di idee scacchistiche, anche se non ha esaurito tutte le verità e non ha detto solo verità. Ma è veramente importante esaurire tutte le verità scacchistiche e ed è quello che avremmo desiderato da un sistema? Che gusto ci sarebbe a giocare se avessimo un sistema limitato di regole che dimostra tutte le verità?

Chiudo riallacciandomi alla citazione iniziale del mio amato Orson Welles. La logica rimane una delle discipline che ha rivoluzionato il mondo e che ha illuminato addirittura sui limiti della nostra conoscenza. Ma la logica rimane una parte infinitesima di quello che la mente umana è in grado di produrre. Beethoven, il mio più grande ispiratore e che considero, con Kant, mio padre putativo, odiava il metronomo perché riteneva che dalla sua meccanicità non si producesse alcun che di intelligente e, non a caso, l’ottava sinfonia è uno sberleffo alla meccanicità che sembra dire “vedi un po’ tu, orologio, se riesci a seguirmi”: in un certo senso, un “gödeliano” ante litteram! E allora ben vengano gli scorpioni che, pur essendo logici, non possono fare a meno del loro carattere! Ben vengano gli scacchisti logici, ma che non perdano il loro carattere di scacchisti!

Colgo l’occasione per specificare che questa presentazione non è logicamente rigorosa, e non vuole essere una dimostrazione formale ma vuole solo far vedere come si può usare la logica per parlare di scacchi e come, in fin dei conti, la logica non sia tutto!

Segnalo che a breve uscirà il mio libro sulla filosofia degli scacchi nella quale i temi qui trattati ricevono uno spazio piuttosto ampio, sia nel primo che nell’ottavo capitolo. Tuttavia, questo saggio rimane indipendente da essi.

Per quanto una persona possa scrivere un articolo, buono o cattivo che sia, egli è sempre debitore di una ristretta cerchia di individui senza i quali non avrebbe mai potuto concepire le sue idee e i suoi pensieri che, poi, diventano un tutto organico. Secondo molti filosofi e, secondo me, con molte ragioni, la gratitudine è un’importante virtù morale che è spesso disattesa per orgoglio individuale, stupidità morale e superficialità sentimentale. Io, invece, sono felice di essere grato ad alcune persone, perché attesta la ricchezza del mondo (del mio) e del fatto che nessun’idea nasce da sola.

Desidero, in questa sede, ringraziare a vario titolo almeno due persone che, con la loro disponibilità, amicizia e intelligenza, hanno fatto ciò che i libri non hanno potuto: mi hanno aiutato a farmi un’idea e a cambiare opinione sul mondo. Non sarò mai in grado di ringraziare abbastanza Stefano Sabatini, una persona che ha segnato il mio percorso umano e filosofico, imponendomi all’attenzione della mia mente ancora giovane ciò che essa avrebbe irrimediabilmente rifiutato. Così ringrazio anche Francesco Marigo per le diverse discussioni, suggerimenti e aiuti; una persona il cui intelletto vigile ha consentito a lui di diventare più volte campione italiano di Go e profondo studioso di matematica, e a me di avere un amico intelligente, il risultato ormai insperato di anni di ricerca.

Infine ringrazio voi, lettori, per avermi dato sempre un sostegno duraturo per quelli che, altrimenti, sarebbero solo degli argomenti per dotti.

Segnalo, qui, solo i libri che direttamente contribuiscono ad una chiarificazione dei problemi trattati di logica e di scacchi. Non ho intenzione di fornire una bibliografia più estesa per la semplice ragione che includerebbe moltissimi lavori che fuorvierebbero quella che potrebbe essere una ricerca mirata del lettore.

Berto F., Logica da zero a Gödel, Laterza, Roma-Bari, 2007.

Berto F., Tutti pazzi per Gödel, Laterza, Roma-Bari, 2008.

Carlucci Aiello L., Dapor M., Intelligenza Artificiale: i primi 50 anni, Mondo Digitale., Giugno 2004.

Chomsky N., Linguaggio e problemi della conoscenza, Il mulino, Bologna, 1998.

Chomsky N., Three models for the description of language. www.chomsky.info.

Ciancarini P., Il computer gioca a scacchi, Mondo Digitale, settembre 2005.

Ciancarini P. I giocatori artificiali, Mursia, Milano, 1991.

Frege G., Ricerche logiche, Guerini e Associati, Milano, 2004.

Halmos P. R. (1960), Teoria ingenua degli insiemi, Feltrinelli, Milano, 1976.

Hammer E., Peirce’s Logic, http://plato.stanford.edu/entries/Peirce’slogic/.

Hofstadter D., Gödel, Escher e Bach. Una Eterna Ghirlanda Brillante, Adelphi, Milano, 2003.

Gardner M., Enigmi e giochi matematici, Enciclopedie Pratiche Sansoni, Firenze, 1972.

Nimzowitsch A., Il mio sistema, Caissa, Roma, 2005.

Oriolo P., Coda A., Algebra e informatica, Voll. I., Bruno Mondadori, Milano.

Palladino D., Corso di logica. Introduzione elementare al calcolo dei predicati, Carocci, Roma, 2005.

Russell, B., The principles of mathematics, Newton Compton, Roma, 1989.

Connectionism. First published Sun May 18, 1997; substantive revision Wed Mar 7, 2007.

Turing A. M., Intelligenza Meccanica, Bollati Boringhieri, Milano, 1994.

Wittghenstein, L., Tractatus Logico-philosophicus, e Quaderni 1914-1916, Einaudi, Torino, 1998

Giangiuseppe Pili

Giangiuseppe Pili è Ph.D. in filosofia e scienze della mente (2017). E' il fondatore di Scuola Filosofica in cui è editore, redatore e autore. Dalla data di fondazione del portale nel 2009, per SF ha scritto oltre 800 post. Egli è autore di numerosi saggi e articoli in riviste internazionali su tematiche legate all'intelligence, sicurezza e guerra. In lingua italiana ha pubblicato numerosi libri. Scacchista per passione. ---- ENGLISH PRESENTATION ------------------------------------------------- Giangiuseppe Pili - PhD philosophy and sciences of the mind (2017). He is an expert in intelligence and international security, war and philosophy. He is the founder of Scuola Filosofica (Philosophical School). He is a prolific author nationally and internationally. He is a passionate chess player and (back in the days!) amateurish movie maker.

View all posts