
Run out and find me a four-year-old child. I can’t make head or tail out of it. – Groucho Marx
Introduction to Emoji Logics and Caveats
For many years I studied formal logics and set theory alongside everything else. They were the intrinsic foundation of my background work, the one that never appeared on the surface because it was too personal and too specific at the same time.[1] Moreover, in spite of many applications of formal logic thinking from war to society, I never fully embraced the sheer love for machinery or formal symbolism because I am much more semantically driven.[2] In fact, I am obsessed by semantics and natural language and the more I think about them the deeper the obsession. Although I have been always skeptical on analytic philosophy implicitly share belief that it is all about bad use of unclarified language and truth-values, I am in fact as obsessed as the later Wittgenstein or Kant in the three major critiques, which are essentially a quest for understanding how our judgements (statements) is even possible. In fact, I even argued that the deconstruction of judgement through language was ultimately what Kant achieved in the Critique of Pure Reason.[3]
However, this does not change my sheer admiration for those pillars of thought who elaborated formal logics how we know it and Kurt Godel has been my logical hero since I started my logical quest twenty-four years ago.[4] As a result of my effort to teach formal and informal logics, I arrived to conceive an idea to how teach basic principles of formal logics to kids. I am not very versatile with very young kids, that is, less than 14 and I don’t have any evidence of specific applications of the system I am proposing here, but the idea is very simple. Formal logic is about creating a system of codified symbols to be manipulated syntactically, that is, through the ‘simple’ application of rules, we can be creative in selecting what symbols we want to use. What if we are creative and use emoticons for formalizing propositional logic?
With this intuition in mind, I propose the following formal logic game that could be used for teaching logic to kids. I welcome any reader to try and report what happened and how it worked in the comments section.
Formalization of the Emoji Logics – Propositional Logic in Emoticons
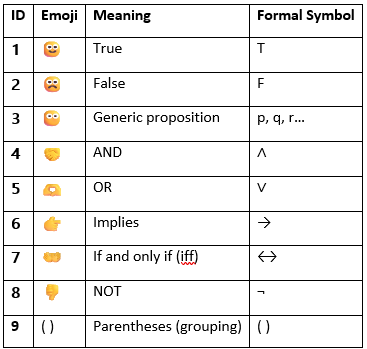
It should be sufficiently apparent why I called the system ‘Emojis Logics’ after going through the process of formalization. The following matrixes are the classic transposition of propositional logic into a set of symbols to be interpreted according to classic logical rules. I used the classic symbology associated with an emoji I felt appealing. For example, the generic proposition is a face without a smile to suggest that it can be either way: happy (true) or sad (false).
Propositional connections such as AND and OR are visualized as a shake hands for the AND because it unites where, instead, the OR is a heart for suggesting that there is more room for agreement. Instead, I used the finger pointed for material implication because it is very similar to the original arrow. IFF is rendered through the two hands to suggest that the implication is directed in both directions. However, possibly a better symbol can be found. NOT is rendered through the thumb down for sufficiently obvious reasons! Finally, the parentheses are untouched because they are not technically part of the language and, more importantly, help the readability as they are and they can be immediately compared to basic arithmetic operations that the kids could be already familiar.
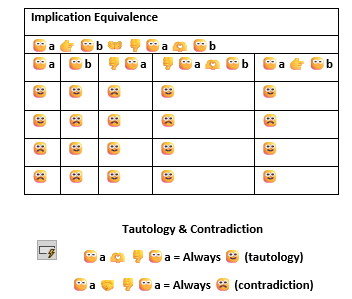
Interestingly, this system could shed light into why humans codify faces or physical gestures in the way in which they do. There is a clear need for signaling validation and agreement or the opposite. There is also a clear need for suggesting conjunctions or disjunctions of emotions or interests (shake hands and heart). Similarly, negation is such a fundamental necessity for inverting the truth-value of a given statement that having a way to communicate it is useful. Interestingly, there is a widespread redundancy across emojis and equivalent gestures for similar operations such as negation, approval, agreement and validation. In this sense, as Frege would have said, different smiles suggest different ways to express the same propositional content or even truth-value. This seems to indicate that we still build on top of those core connectives and logical principles, which means that the process of emotional association follows and not start from logics or general rationality, although the premises of natural arguments can be emotionally driven. Funnily enough, tautologies are interpreted as ‘always smiling faces’, which immediately show that tautologies are trivial, and contradictions are intrinsically wrong.
Thanks to this simple rendering, we have translated all the classic symbols of propositional logic. A similar process can be done for predicative logic, but this would go possibly too far and for the moment, this is only proof of concept.
Importantly, for discriminating against the propositions, different colors will be used to differentiate variables in illustrations. This has its own limitations as colors are finite, and propositions are not. But I bet that young kids (and older folks as well) could struggle in dealing with the infinite and, of course, in practice we don’t write infinite series of propositions. As a result, five to ten colors will work just fine.
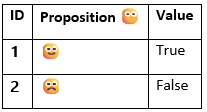
Truth Value Matrix for Emojis Logics Propositions
Now that we have the symbology machinery, we are ready to apply it to all the rest of our emoji-formal logic system or Emoji Logics. Firstly, we codify specifically what symbols we want to use for the truth values, true and false.
With all the symbology defined, we are now ready to move on for the logical operator definitions with a truth-table. The table includes all the classic logical connections.

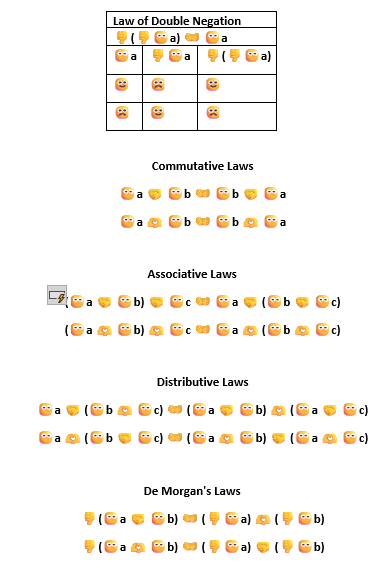
Key Logical Laws in Emoji Logic with Truth Tables in Emojis Logics
Emoji Logic is now ready for expressing logical laws such as the law of double negation, commutative laws, associative laws, distributive laws, implications equivalence, tautologies and contradictions.
There are fascinating ideas that can be created with systems. For example, it could be interesting to try to reduce all the other emojis to these fundamental ones. This would teach the principle of substitution to kids and to show that everything can be reduced to more fundamental principles and conditions. This could have specific interesting applications. For example, if we use Emoji Logic to render a system of natural deductions, we could use a specific smile for propositions that were once part of an argument and now discharged as part of a conclusion of another given argument.
[1] Beyond certain specific sections of published works and papers.
[2] For example, see Pili, G., ‘Natural language and set theoretical and formal logic reductions’, Scuola Filosofica, 2024, available at: https://www.scuolafilosofica.com/12145/natural-language-and-set-theoretical-and-formal-logic-reductions or my commentaries on Wittgenstein, Russell, Frege etc..
[3] Pili, G., ‘Kant affronta il paradosso dell’analisi’, Scuola Filosofica, 2019, available at: https://www.scuolafilosofica.com/7675/6-kant-affronta-il-paradosso-dellanalisi
[4] Pili, G., ‘Cosa ne pensava davvero Kurt Gödel?’, Scuola Filosofica, 2015, available at: https://www.scuolafilosofica.com/4831/cosa-ne-pensava-davvero-kurt-godel




Be First to Comment