Iscriviti alla Newsletter!
Consigliamo – Percorso di filosofia antica
Vita
Se di qualche presocratico si ha qualche cenno biografico, così non è per Zenone di Elea del quale si sa solo che fu amico e discepolo di Parmenide, rispetto al quale era di venticinque anni più giovane. In base a ciò la sua vita si può datare tra il V secolo a.C., si può supporre che nacque attorno al 490-480, date sino ad un certo punto indicative.
Scrisse un’opera di cui abbiamo cinque frammenti e questa, a differenza che il trattato di Parmenide, era in prosa.
Schema di ragionamento
Ipotesi Z(enone) 1: l’essere è.
Corollario I: ne consegue che l’essere è uno dalla sua sola definizione.
Specifica a: come detto, Zenone si limita a prendere le tesi del suo maestro, Parmenide, e dimostrarle. Dunque, le ipotesi fondamentali non sono sue originarie ( 1, 2… ) ma del maestro. Ciò che c’è di originale e, se vogliamo, rivoluzionario e geniale in Zenone è il suo procedimento dimostrativo, diventato celebre e del quale ancora oggi si fa uso sovente, seppure non applicato al movimento e all’apparenza.
Ipotesi Z2: il non-essere non-è.
Specifica a: il non-essere è la molteplicità. Molteplicità implica tanto variazione di qualità e quantità, quanto di spazio e tempo. Molteplicità è il fenomeno così come appare alla sensibilità. Ma ormai, tutte questo cose, già le sappiamo.
Inferenza: Se l’essere è, se l’essere è uno, se la molteplicità è non essere allora la molteplicità non esiste.
Tesi ZI: dunque la molteplicità non esiste.
Dimostrazione: se ammetto che esiste la molteplicità allora mi contraddico. La molteplicità ( semplifichiamo ) è qualificata sostanzialmente dal movimento. Se dimostro che non esiste il movimento allora dimostro che non esiste molteplicità.
P(asso dimostrazione)1: esiste un corpo in uno spazio.
P2: il corpo deve compiere un percorso, il percorso è definito dal segmento ( tratto ) AB.
P3: il corpo da A deve raggiungere B.
P4: il corpo per raggiungere B deve prima percorrere la metà della distanza ( AB/2 ovvero AB · ½ )
P5: il corpo per raggiungere la metà del segmento deve prima raggiungere la metà della metà del segmento ( AB/4 ovvero AB · ½ · ½ )
P6: il corpo per raggiungere B deve prima percorrere la metà della metà della metà del segmento ( AB/8 ovvero AB · ½ · ½ · ½ ).
Il P4 va ripetuto infinite volte: il corpo non sarà mai in grado di raggiungere B e sarà fermo. La grandezza che assume il segmento percorso da B tende a zero in quanto il procedimento della divisione per due non solo è infinito ma tanto più è operato e tanto più diminuisce la quantità di spazio percorribile dal corpo. Così la grandezza del segmento percorribile diminuisce all’aumentare delle volte con cui io ripeto il P4.
Sono riuscito a dimostrare che il corpo non raggiungerà mai la sua destinazione, dunque il movimento non esiste così l’essere è uno e la molteplicità non esiste.
Specifica a: la dimostrazione si basa sull’idea che se confuto il contrario di ciò che affermo, allora ciò che affermo rimane vero. O è vero un enunciato o è falso. Se dimostro che la falsità di un enunciato è falsa allora non rimane che affermare la sua verità. In ciò sta la natura del ragionamento per assurdo: per-assurdo proprio perché passa-attraverso l’assurdità.
Specifica b: Zenone arriva a dimostrare che il moto non esiste impostando il problema in modo tale che uno dei passi della dimostrazione implichi una sua ripetizione infinita. Ovvero ogni qual volta si segue il metodo suggerito si deve (ri-)iniziare ciò determina che l’inizio e la fine del problema si rimandino e, in altre parole, il problema dal principio alla fine della dimostrazione rimane inalterato. Infatti Zenone non ha certo intenzione di risolvere il problema del moto, egli si limita semplicemente ad affermare, non la sua falsità ma addirittura la sua insensatezza. Il problema del moto è un problema inesistente.
Specifica c: non si può non notare una cosa: Zenone non si interessa alla definizione del moto, egli parla in generale di un corpo che si sposta senza analizzare la questione in termini di definizione. Ciò che egli arriverebbe a dimostrare è solo che un segmento è sempre divisibile per due. Egli dunque non ha certo in mente di stabilire nulla, si limita ad affermare che ci sbagliamo quando pensiamo che l’essere sia molteplice.
Schema grafico
P(asso dimostrazione)1: esiste un corpo in uno spazio.

P2: il corpo deve compiere un percorso, il percorso è definito dal segmento ( tratto ) AB.
 P3: il corpo da A deve raggiungere B.
P3: il corpo da A deve raggiungere B.

P4: il corpo per raggiungere B deve prima percorrere la metà della distanza ( AB/2 ovvero AB · ½ )
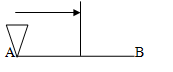
P5: il corpo per raggiungere la metà del segmento deve prima raggiungere la metà della metà del segmento ( AB/4 ovvero AB · ½ · ½ )
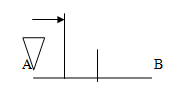
P6: il corpo per raggiungere B deve prima percorrere la metà della metà della metà del segmento ( AB/8 ovvero AB · ½ · ½ · ½ ).
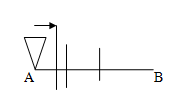 Ricordiamo che tale procedimento è valido anche per comprendere tutti gli altri paradossi. Basta che si sostituisca alla “quantità di spazio” un’altra “quantità”: tanto ogni quantità si può dividere per due infinite volte.
Ricordiamo che tale procedimento è valido anche per comprendere tutti gli altri paradossi. Basta che si sostituisca alla “quantità di spazio” un’altra “quantità”: tanto ogni quantità si può dividere per due infinite volte.
Filosofia
Aristotele lo considera il padre della dialettica per il suo modo di impostare le questioni. Zenone fu il primo ad utilizzare la tecnica argomentativa della reductio ad absurdum ( riduzione all’assurdo ) la quale prevede l’assunzione della tesi dell’avversario per mostrarne la contraddizione.
Tutta la riflessione di questo grande filosofo non fu positiva, nel senso non che non propose né aggiunse nulla rispetto al pensiero del suo maestro, Parmenide, come fece Melisso, piuttosto si limitò ad argomentare a favore delle tesi di Parmenide. Egli si impegnò a dimostrare che le tesi degli avversari erano assurde, venendo così a confermare le idee della teoria parmenidea.
Se il maestro si scagliò contro i dati dell’esperienze, è naturale che avrebbe trovato molti scettici intorno a tale riduttiva visione dell’esperienza: ciò causava infatti la demolizione del senso comune che nasce proprio dall’accettazione della molteplicità.
Questa, come si è già detto, ha come caratteristiche fondamentali la possibilità di movimento, la mutevolezza dello spazio e del tempo e le distinzioni. Zenone espose quaranta paradossi a favore delle tesi di Parmenide attraverso dimostrazioni per assurdo. La parola “paradosso” nasce dall’unione di due vocaboli greci “para” ( contro ) “doxa” ( opinione ).
Per i paradossi della molteplicità:
1) Se vi sono più cose, allora sono simili in qualcosa ma sono anche dissimili ( dunque sono e non-sono ).
2) Se vi sono più cose allora ogni cosa è limitata e infinitamente estesa.
3) Se vi sono più cose allora sono infinite di numero e finite di numero.
Per quanto riguarda lo spazio:
- Se ogni cosa che esiste è in uno spazio allora esiste lo spazio, ma lo spazio sarà in uno spazio che sarà in uno spazio ecc..
Per quel che riguarda i paradossi dell’illusorietà della molteplicità:
- Se un chicco di grano non fa rumore se cade, allora neanche cento chicchi di grano fanno rumore se cadranno.
I paradossi sull’impossibilità del movimento sono quattro e tutti si basano sull’infinita divisibilità dello spazio:
I. Un corpo in movimento rispetto ad un corpo fermo: il corpo “A” non si muoverà perché dovrà prima di tutto muoversi per l’intera metà dello spazio da percorrere. Ma dovrà anche farlo per la metà della metà, così per la metà della metà della metà ecc..
II. Due corpi in movimento rispetto l’uno verso l’altro: i corpi “A” e “B” non si raggiungeranno mai perché entrambi devono compiere la metà dell’intero percorso, ma prima la metà della metà ecc..
III. Due corpi a velocità diversa ma verso la stessa direzione ( Achille e la Tartaruga ); il corpo più veloce è posto prima del corpo più lento: i due corpi non si toccheranno mai perché il corpo più veloce dovrà compiere metà del tragitto tra sé e il corpo più lento. Ma il corpo più lento nel mentre si sarà spostato, seppur di poco, così il corpo più veloce oltre al resto del tragitto dovrà spostarsi anche di quel tanto che l’altro corpo si è spostato, ma nel mentre che compie questo spostamento anche l’altro corpo, per quanto lento, si sarà nuovamente spostato: il procedimento sarà così infinito e i due corpi non si raggiungeranno mai.
La logica alla base dei tre paradossi sul movimento è sempre la stessa, ovvero un corpo non si muoverà mai perché dovrà sempre percorrere la metà della metà etc. e, dunque, si annulla il movimento: XY/2 · ½ · ½ ( dove XY sono gli estremi del segmento )[1]…
Riferimenti
Aristotele, Organon. Adelphi. Milano A cura di Giorgio Colli. Pp. 252, 628, 675, 707, 720.
« La frase: la falsità non deriva da questo, che ci accade spesso di pronunciare nelle discussioni, si applica fondamentalmente ai sillogismi che conducono all’assurdo, quando serva a contraddire ciò che è stato provato con la riduzione all’assurdo. In effetti, chi non voglia esprimere tale contraddizione, non dirà: la falsità non deriva da questo, bensì dichiarerà falsa qualcuna delle proposizioni stabilite in precedenza; d’altro canto, tale frase non verrà pronunciata neppure nel caso della dimostrazione diretta, dato che questa prova non pone qualcosa, che debba venir contraddetto nella conclusione. Oltre a ciò, quando una proposizione sia stata demolita probativamente, mediante i termini A, B, C, non è possibile dire che il sillogismo non si sviluppa da ciò che è stato assunto. In realtà, noi diciamo: la falsità non deriva da questa proposizione, quando, una volta eliminata la proposizione, il sillogismo giunge non meno di prima alla sua conclusione, il che per l’appunto non può avvenire nel caso dei sillogismi probativi. Qui difatti, una volta eliminata la proposizione inizialmente assunta, anche il sillogismo che la concerne, fondandosi su di essa, non sussisterà più. Risulta dunque evidente, che l’espressione: la falsità non deriva da questo, si applica ai sillogismi che conducono all’assurdo; più precisamente, essa potrà venire usata, quando l’ipotesi iniziale sta rispetto alla conclusione assurda in un rapporto tale, che la necessità di tale conclusione risulta invariata, sia che l’ipotesi sussista, sia che non sussista.
Orbene, il caso più evidente, in cui la conclusione falsa non deriva dalla proposizione inizialmente assunta, si presenta quando la concatenazione sillogistica, che dai medi conduce all’assuro, non si collega all’ipotesi (…). In realtà, il fissare come causa ciò che non è causa consiste in ciò, e si verifica, ad esempio, quando qualcuno, volendo provare l’incommensurabilità della diagonale, metta mano all’argomentazione di Zenone, che conduce all’impossibilità del movimento, e consideri tale conclusione come assurda: la conclusione falsa di fatti non si collega assolutamente, in alcun modo, con l’affermazione iniziale ».
« … in realtà, noi possiamo disporre di molte argomentazioni, che si contrappongono alle opinioni correnti e sono difficilmente risolubili, ad esempio delle argomentazione di Zenone, secondo cui nulla può muoversi né percorrere lo stadio, ma non per questo si dovrà rifiutare l’assenso alle premesse che si contrappongono a tali discorsi. Concludendo, se chi risponde non concede la premessa, senza disporre né di un’obiezione né di un argomento per contrattaccare è chiaro che non rispetta le regole di una corretta discussione…»
« … si può dire ad esempio che ciò che è, o ciò che è uno, abbia parecchi significati, eppure in una certa occasione tanto la persona interrogata quanto Zenone, che interrogava, pensavano ad un unico significato, da che risultò un discorso, per provare che tutte le cose sono una sola… »
« In realtà si può mostrare che il sillogismo ha dedotto una conclusione falsa, senza mostrare quale sia la premessa onde questa deriva, come avviene ad esempio rispetto all’argomentazione di Zenone, secondo cui il movimento è impossibile… »
« …Alcuni infatti pensano che ciò che è e rispettivamente l’uno abbiano sempre lo stesso significato; altri invece risolvono la prova di Zenone e di Parmenide, affermando che l’uno e è ciò che è si dicono in più sensi… »
Kant I. Critica della ragion pura. Laterza, Roma-Bari. Lib. II, Cap. II, Sez. VII. P 331.
« … Zenone di Elea, sottile dialettico, fu già da Platone biasimato come petulante sofista, perché, egli, per dar prova della sua arte, cercava di una stessa proposizione, di dimostrarla per mezzo di speciosi argomenti, e subito dopo abbatterla con altri argomenti altrettanto forti. Egli affermava che Dio ( che probabilmente per lui non era altro che il mondo ) non è né finito né infinito; non è né in movimento né in moto né in quiete; non è né simile ad altra cose né dissimile. A quelli che lo hanno giudicato su questo su questo, è sembrato che egli abbia voluto negare affatto due proposizioni tra loro contraddittorie, ciò che è assurdo. Ma io non trovo che si abbia ragione a mettergli carico quest’assurdo. Illustrerò ora, più da vicino, la prima di queste proposizioni. Per ciò che riguarda le rimanenti, se con la parola di Dio egli intese l’universo, egli doveva certamente dire, che questo né è costantemente presente nel suo luogo ( in quiete ), né cangia luogo ( si muove ), perché tutti i luoghi sono nell’universo e questo stesso, dunque, non è in nessun luogo. Se l’universo comprende in sé tutto quello che esiste, esso altresì per tanto non è simile a un’altra cosa, né dissimile, perché fuori di esso non c’è altra cosa, con la quale possa essere paragonato. Se due giudizi fra loro opposti presuppongono una condizione impossibile, cadono entrambi, malgrado la loro opposizione ( che intanto non è una vera e propria contraddizione ), perché non ha luogo la condizione alla quale soltanto ciascuna di queste proposizioni dovrebbe essere valida ».
Goedel, Escher, Bach: una Eterna Ghirlanda Brillante. Douglas R. Hofstadter. Gli adelphi. P. 31-34, 156, 659.
« Achille: Che cos’è quella strana bandiera dall’altro lato della pista? Mi ricorda inqualcosa una stampa del mio artista preferito, M. C. Escher.
Tartaruga: Quella è la bandiera di Zenone.
Achille: Il foro che c’è non somiglia a quelli disegnati da Escher in un suo nastro di Mobius? Qualcosa non va in quella bandiera. Ne sono certo.
Tartaruga: L’anello che è stato ritagliato nella bandiera ha la forma di uno zero, che è il numero preferito di Zenone.
Achille: Ma lo zero non è stato ancora inventato! Verrà inventato tra qualche millennio da un matematico indiano. E quindi, signorina Tartaruga, ciò prova che la bandiera è impossibile.
Tartaruga: Il suo argomento è convincente, Achille, e io devo convenire che una simile bandiera è davvero impossibile. Comunque, è bella, non è vero?
Achille: oh, sì, non c’è dubbio alcuno sulla sua bellezza.
Tartaruga. Mi chiedo se la sua bellezza non sia connessa con la sua impossibilità. Non lo so; non ho mai avuto il tempo di analizzare la Bellezza. La Bellezza è una Essenza Maiuscola, e sembra che io non abbia mai tempo per le Essenze Maiuscole.
Achille: Parlando di Essenze Maiuscole, signorina T., si è mai interrogata sullo Scopo della Vita?
Tartaruga: Cielo, no!
Achille: Non si è neanche chiesta mai come mai siamo qui, chi ci ha inventati?
Tartaruga: Oh, questa è una cosa del tutto diversa. Noi siamo invenzioni di Zenone ( come presto scoprirà ) e la ragione per la quale siamo qui è che dobbiamo misurarci in una gara podistica.
Achille: Una gara podistica? Che insolenza! IO, il più veloce di tutti i mortali, misurarmi con lei, l’essere più lento di tutti i lenti! Questa gara non può che essere priva di senso.
Tartaruga: Lei potrebbe darmi un po’ di vantaggio.
Achille: Dovrei darle un grossissimo vantaggio.
Tartaruga: Non faccio obbiezioni.
Achille: Ma la raggiungerò, prima o poi, presto o tardi; molto probabilmente, prima.
Tartaruga: No, se le cose andranno secondo il paradosso di Zenone. Zenone spera di usare la nostra gara podistica per dimostrare che il moto è impossibile, capisce? Secondo Zenone, il moto sembra possibile solo nella mente. In verità, il Moto è Interamente e Intrinsecamente Impossibile. Ed egli lo dimostra in maniera davvero elegante.
Achille: Oh, mi ricordo adesso: il famoso koan Zen sul Maestro Zen Zenone. Come dice lei, è davvero molto semplice.
Tartaruga: Koan Zen? Maestro Zen? Che dice?
Achille: Dice: due monaci stavano discutendo di una bandiera. Uno disse: “La bandiera si muove”. L’altro disse: “E’ il vento che a muoversi”. Zenone, il sesto patriarca, stava passando per caso da quelle parti. Egli disse loro: “non il vento, non la bandiera; è la mente che si muove”.
Tartaruga: Ho l’impressione che lei faccia un po’ di confusione, Achille. Zenone non è un maestro Zen; tutt’altro. Egli è, in verità, un filosofo greco della città di Elea ( che sta a metà strada fra il punto A e il punto B ). Nei prossimi secoli sarà famoso per i suoi paradossi sul moto. In uno di questi paradossi la gara podistica che lei e io dovremo affrontare ha il ruolo centrale.
Achille: sono veramente perplesso. Ricordo perfettamente che mi ripetevo di continuo i nomi dei sei patriarchi Zen e dicevo sempre: “il sesto patriarca è ZZ… enone, il sesto patriarca è ZZ… enone…” ( improvvisamente si leva una leggera, tiepida brezza ). Oh, guardi, signorina Tartaruga, com’è bella la bandiera che ondeggia! Che bei giochi di luce vi producono quelle increspature che scivolano lungo il morbido tessuto! Ed anche l’anello che vi è ritagliato ondeggia!
Tartaruga: Non sia ridicolo. La bandiera è impossibile, quindi non può ondeggiare. Il vento ondeggia.
( Compare Zenone )
Zenone: Salve, salve. Che succede? Che c’è di nuovo?
Achille: La bandiera si muove.
Tartaruga: E’ il vento a muoversi.
Zenone: Oh, amici, ponete fine alle vostre diatribe! Fermate la vostra ira! Cessate le vostre discordie! Poiché io risolverò il problema in un attimo. E poi in un giorno così bello!
Achille: Questo è un po’ suonato.
Tartaruga: No, aspetti, Achille, vediamo cosa ha da dire. Oh, sconosciuto, deh, fa’ noi partecipi del tuo pensiero su questo argomento.
Zenone: Con estremo piacere. Non il vento, non la bandiera: nessuno dei due si muove. Né altro si muove. Perché io ho scoperto un grande Teorema che dice: “Il Moto è Interentemente e Intrinsecamente Impossibile”. E da questo Teorema consegue un Teorema ancora più grande, il Teorema di Zenone: “Il Moto Unesiste”.
Achille: “Il Teorema di Zenone”? E’ lei per caso, il filosofo Zenone di Elea?
Zenone: Ebbene, sì. Achille.
Achille: ( grattandosi il mento con un’espressione di stupore ) Come fa costui a sapere il mio nome?
Zenone: Posso persuadere voi due ad ascoltarmi sul perché è così? Ho fatto tutta la strada dal punto A fino ad Elea questo pomeriggio, proprio per tentare di trovare qualcuno disposto a prestare un po’ di attenzione alla mia inattaccabile argomentazione. Ma qui sono tutti indaffarati, e non hanno tempo. Non potete immaginare quanta amarezza si prova quando si riceve un rifiuto dopo l’altro. Oh, mi dispiace di annoiarvi con i miei guai, ma vorrei chiedervi solo una cosa: sareste disposti noi due a compiacere un vecchio, ridicolo, filosofo?, ascoltandolo per pochi attimi, solo pochi davvero, appena il tempo necessario per esporre le sue eccentriche teorie?
Achille: Oh, ma certo! Prego, ci illumini! Io so che parlo per entrambi poiché la mia amica Tartaruga stava proprio parlando di lei poco fa con grande venerazione e ha accennato in particolare ai suoi paradossi.
Zenone: Grazie. Vedete, il mio Maestro, il quinto patriarca, mi ha insegnato che la realtà è una, immutabile ed eterna; tutta la pluralità, il divenire e il moto sono mere illusioni dei sensi. Alcuni si sono presi gioco delle sue idee; ma io mostrerò l’assurdità di questo atteggiamento irriverente. Il mio argomento è molto semplice. Lo illustrerò con due personaggi di mia Invenzione: Achille ( il guerriero greco più veloce di tutti i mortali ) e una Tartaruga. Nel mio racconto essi vengono convinti da un passante a fare una gara podistica lungo una pista verso una bandiera che sventola nella brezza. Supponiamo che la Tartaruga, visto che molto pià lenta, si prenda un vantaggio, diciamo di una decina di pertiche. Ora la gara ha inizio. In pochi balzi Achille ha raggiunto il punto di partenza della Tartaruga.
Achilla: Ah!
Zenone: Ed ora la Tartaruga ha solo una pertica di vantaggio su Achille. In un solo attimo Achille percorre questa distanza.
Achille: Eh, eh.
Zenone: Tuttavia in quel breve attimo la Tartaruga è riuscita a fare un piccolo balzo in avanti. In un baleno Achille copre anche quella distanza (…). Ma in quel brevissimo tempo la Tartaruga sarà riuscita ad avanzare ancora di un pollice. E così Achille è ancora indietro. Ora capite perché Achille raggiunga la Tartaruga, questo gioco deve essere giocato un numero INFINITO di volte; e quindi Achille non raggiungerà MAI la Tartaruga!
Tartaruga: oh, oh, oh!
Achille: Hum, hum, hum… Questo ragionamento ha qualcosa che non và. E tuttavia non riesco ad individuarne l’errore.
Zenone: Non è un rompicapo? E’ il mio paradosso preferito!
Tartaruga: Ma scusami, Zenone, il tuo racconto riguarda un altro principio, no? Tu hai appena finito di raccontarci ciò che sarà nonto tra molti secoli come “il paradosso di Achille” secondo il quale Achille (ehm) non raggiungerà mai la Tartaruga; ma la dimostrazione che il Moto è Inerentemente Intrinsecamente Impossibile ( e che quindi il Moto Unesiste ) è il tuo “paradosso della dicotomia”, no?
Zenone: Oh, che vergogna! Naturalmente volevo raccontare l’altro paradosso. Quello che dice che per andare da A a V si deve prima percorrere la metà della strada e poi un’altra metà di quella che rimane da percorrere e così via. Il fatto è che entrambi questi paradossi hanno la stessa natura. Francamente, io ho avuto una sola Grande Idea. E l’ho sfruttata in diversi modi.
Achille: Giuro che questi ragionamenti hanno un tallone d’Achille, non so bene dovbe, ma certo non possono essere giusti.
Zenone: Lei dubita della validità del mio paradoss? Perché non prova e vede quella bandiera rossa laggiù, alla fine della pista?
(…)
Che ne dite di una corsa sin laggiù? »
« Quando è consentito agli elettroni e ai fotoni nudi di interagire secondo questi modi arbitrariamente aggrovigliati, si ottengono elettroni e fotoni rinormalizzati. Perciò, per comprendere come un elettrone si propaghi da A a B, il fisico deve saper effettuare una specie di media sull’insieme infinito dei possibili diversi diagrammi in cui figurano particelle virtuali. Ecco Zenone che ricompare ».
« Il fatto che aiuta nella dimostrazione dei teoremi, è che si dispone di obbiettivo globale, cioè di la stringa che si vuole produrre, con la quale ci si può orientare localmente. Una tecnica elaborata per convertire obiettivi globali in strategie locali per le derivazioni in corso è chiamata riduzione a sottoproblemi. (…)
La riduzione a sottoproblemi portò Zenone al disastro. Il metodo di Zenone per andare da A a B ( si pensi a B come la meta ) consiste, come si ricorderà., nel “ridurre” il problema a due sottoproblemi: per percorri metà della strada, poi l’altra metà. Ora in questo modo si sono (…) inseriti questi obiettivi secondari nella nostra “pila obbiettivi”. Ciascuno di questi a sua volta sarà sostituito da altri due obbiettici di terzo ordine, e così via, all’infinito. Ci si ritrova con una pila di obbiettivi infinita anziché con un singolo obbiettivo. Eseguire un numero infinito di obiettivi [ la parola obbiettivi sostituisce quella di “pop” del testo originario N.D.R. ] dalla pila si dimostrerà un compito impossibile; ed è appunto questo l’argomento di Zenone ».
Nostra bibliografia essenziale
Per avere un quadro generale del filosofo, suggeriamo la lettura de “Manuale di storia della filosofia I” di Gregory, Verra e Adorno, in generale uno dei manuali più chiari e con ottime bibliografie.
[1] Chiedo scusa per l’assenza della stanga superiore per indicare il segmento ma non è una mia mancanza, piuttosto del mio computer!





Be First to Comment